陈省身证明高斯博内公式是在预期理由的假设下--无效

陈省身6页纸证明高斯博内公式是在假设下完成，是一种预期理由的错误。预期理由暗含了假定存在的非逻辑前提，数学证明不得使用非逻辑前提。并且，主项还是一个特称判断。这是因为陈省身对逻辑学的无知。
     
    详见论文下面：基于公式（24）,我们将在是闭的-可定向黎曼流形的假设R^n下，给出公式（9）的证明。（即高斯博内公式）。
  
就是说，将黎曼流形分为四种情况：

1，闭的-可定向的；

2，非闭的-不可定向的（高斯-博内公式的核心依赖于?斯托克斯定理?和?奇点指标理论?。在非闭、不可定向的黎曼流形上，原始高斯-博内公式不直接成立，但可通过拓扑转化或边界修正扩展其形式。具体推广需依赖流形的几何和拓扑性质?。）；

3，闭的-不可定向的（公式有效吗？）。

4，非闭的-可定向的（公式有效吗？）。

高斯博内定理的主项只是一个特称判断，

没有包含所有的黎曼流形。有些A是B。

数学定理必须是全称判断即一切A是B。

全称判断的主项是普遍概念或者单独概

念，高斯博内定理主项A没有包括其它3种

情况，就不是普遍概念；那么就可以争取

是单独概念，如果让A即”闭的-可定向的

“成为单独概念，就必须排除其它3种，即

排除：

第一种“非闭的-不可定向”，

第二种“闭的-不可定向的，

”第三种“非闭的-可定向的”。

我们用：

黑色表示“闭的”；

黄色表示“非闭的”；

红色表示“可定向”，

绿色表示“不可定向”。


下图是说，

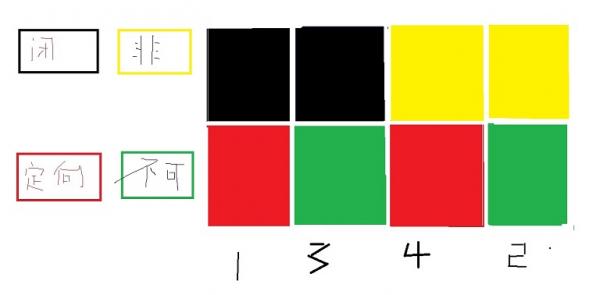
1不能与3和4有重叠（相同颜色），才能是

单独概念，A才能不算特称判断，可以算一

个类。与总体是一个种属关系。

假设造成了命题主项的不确定性。

 




我们是不是太刻薄了？

高斯-博内公式的核心依赖于?斯托克斯定理和?奇点指标理论。在非闭、不可定向的黎曼流形上，原始高斯-博内公式不直接成立，但可通过拓扑转化或边界修正扩展其形式。具体推广需依赖流形的几何和拓扑性质?。

非要让一个定理从头到脚讲清楚？如果我们假设1+1=2，...，推导出4+5=9，就不能算是证明，这是预期理由的错误！

必须有一个皮亚若公理在前面，我们可以推出4+5=9.。

所以，陈省身的证明无效！
人永远需要理由，解释永远需要解释来解释。数学家用公理把数学推理的无穷退后阻断，防止无休止的循环论证。公理让数学有了合法性。

这里有一个充足理由律：a真，因为b真并且b能够推出a。b是a成立的充足理由。就是一个正确思想赖以成立的正确根据。充足理由必须有真实性和相关性。

假设下的证明，就失去了充足理由。

      命题是什么，命题蕴含了概念和概念的关系，它是词项和连接词组成的事物。表征了外部世间事件的对象，以及对象之间的关系、于是就有了知识，概念是数学的核心。

       我们发现，只要符合某些规则，就可以从一个命题推出另外一个命题，从一个断言推出另外一个断言，我们把这个过程叫做推理。

我们又把那个大规模的推理，那个更加系统的推理叫做论证。

于是，我们的语言和知识的范畴不断扩大，结下了一张命题的网络——断言之网。我们通过断言之网理解我们的世界。

       逻辑的合法性来自于形式的合理性，而形式的合理性来自于实践的有效性。溯因达到严格的推理-论证才能叫做定理。

         在这里必须是没有任何模糊性，论证中的一切推理应该井井有条，一切细节环环相扣。结论的正确性建立在前提的正确性和真实性基础上。陈省身的证明没有正确的前提，他的前提是一个没有证明的假设，支撑证明的有效性，是前提的有效。当你的前提无效时，结论就不是可靠的。就不能算是定理。