浅谈量子计算机-1
**** 1. 前言 ****
计算机技术的发展有目共睹。回味计算机历史饶有趣味,1946年诞生的世界第一台电子数字计算机:体重30吨,占地面积170平方米,看起来像一栋大房子。70多年过去了,如今的科学技术,已经将这个庞然大物缩小到装进我们的口袋里。
人类的好奇心和探索精神永无止境。科学家尤其如此,他们并不满足于传统计算机,总是异想天开,企图另辟蹊径,希望解决某些经典计算机无法解决的难题。近几年来,量子计算机这个新名词逐渐进入了人们的视野。那么,什么是量子计算机呢?它和经典计算技术有何不同?有哪些优越性?进展情况如何?
本文简单介绍一下量子计算机,包括基础知识、主要算法,以及物理实现、发展概况等。
**** 2. 历史 ****
也许你会感到奇怪 计算机的能力已经如此强大,为什么还要研发量子计算机呢?是科学家们别出心裁多此一举吧?其实是因为经典计算技术中难以解决的“复杂度”问题。
量子计算的起源要追溯到上世纪70年代,计算机科学的发展启发了多位科学家,对此有了初步想法并开始发表文章。除了几位计算机科学家之外,其中物理学家费曼起了重要的作用。费曼正是因为对量子理论的深入理解,才能提出量子计算技术的设想。
那是在1981年 美国MIT的校园里,召开了物理和计算技术“联姻”的第一次会议。费曼作了一个报告,揭开了研发量子计算机的新篇章【1】。费曼提出一个问题:经典计算机可以被用来模拟量子世界吗?答案是否定的 因为在模拟量子现象时,经典计算机的计算量,将随着系统(粒子数N)的增大而指数增加。费曼认为微观世界的本质是量子的,N非常大,是传统计算机在有效时间内解决不了的问题,也就是如前所说的“计算复杂度”问题。
“复杂度”表征的是所需计算量与问题涉及系统变量数N之间的关系。复杂度分时间和空间,时间复杂度指的是所需计算时间T与系统变量数N之间的关系;空间复杂度指所需比特数B与N之间的关系。两者实际上互相关联,我们以时间复杂度为例。
一般来说,计算时间将随着系统增大而增加。但T的增大因问题而异,T与N可以成线性关系,也可能成平方关系,也有可能是随着N指数增长。可以用函数 O(1)、O(N)等等来表示复杂度,即表示T随N增加的快慢。
时间复杂度包括:线性关系O(N)、平方关系O(N2)、立方关系O(N3)等等,最困难的是指数关系:例如O(2N) 【2】。
费曼的设想使得基于量子力学的计算机的研究被提上了科学发展的历程,物理学家和计算机科学家们都一直在努力。20世纪90年代,量子计算机的几类重要算法得以发展。2013年后,诸如加拿大的D-Wave等真实的量子计算系统陆续出现。随着谷歌、英特尔、IBM等大公司的加盟,量子计算机的量子比特数越来越多,谷歌2019年宣称实现量子霸权,2022年底,IBM发布433量子比特量子计算机,此外,这方面中国也不落后。尽管这些成果中不乏商业炒作,但技术上在不断进步,量子计算机逐渐走向实用,也是有目共睹的。
**** 3. 基础 ****
3.1 叠加态
量子计算的方法与经典计算完全不同,两类计算机速度差异的原因来自于量子现象和经典现象物理规律的不同。量子计算基于量子规律。量子规律的精髓是什么?其实可以用一句话来概括:种种奇怪的量子现象都是来自于量子“叠加态” 【3】。
你也许听过最奇怪的量子现象是“纠缠态”和双缝实验,不过实际上,纠缠态也是一种叠加态,是多粒子体系状态叠加产生的效应,而各类“诡异”的双缝实验均可用叠加态解释。
什么是叠加态呢?根据我们的日常经验,一个物体在某一时刻总会处于某个固定的状态。状态可以用位置、速度、相位、能量等物理参数表示。比如我说,我现在在客厅里,或者说,我现在在房间里。要么在客厅要么在房间,这两种位置状态必居其一。然而,在微观的量子世界中却有所不同!微观粒子可以处于一种不确定的状态中。例如电子可以既在A又在B,电子的状态是“A”和“B”两种状态按一定概率的叠加,这种混合状态就是叠加态。
微观量子世界的粒子一般都处于“叠加态”,但是我们却观测不到叠加态!因为“观察测量”的行为将引起所谓“波函数塌缩”或者被诠释为“退相干效应”,即观测之前是叠加态,观测之后叠加态不复存在,“坍缩” 成了一个确定的状态!因此,我们只能“以某种概率“观测到叠加的多个本征态之一。例如,如果盒子中的”薛定谔猫“化身微观粒子,它的状态可以被表示成“死猫”与“活猫”的叠加态。然而,只要你打开盒子观测,叠加态就塌缩了!你有50%的可能性看到“活猫”,50%的可能性看到“死猫”,但你看不到“既死又活”的猫,换言之,你观测不到它们的叠加态!(图3.1)。

图3.1:叠加态和塌缩
如图3.1左上角,是叠加态波函数的公式,也就是:|y> = a|0> + b|1>。
因此,叠加态通常用2分量量子系统来表示,式中的|0>和|1>表示系统的两个本征态。
3.2 量子比特
量子计算与经典计算的主要区别是运算单元:经典计算机基本运算单位是比特,量子计算机基本单位是量子比特。量子比特(Qubit)也叫量子位(元),实质上就是叠加态。
叠加态可以用布洛赫球面来直观描述。什么意思?如上所述,叠加态|y>可表示为两个本征态|0>和|1>的叠加:|y> = C1|0> + C2|1>。这儿的C1,C2是两个复数,因此,本征态|0>和|1>,以及叠加态|y>,都可以看作是两维复数(希尔伯特)空间中的矢量。两维复空间对应于4维欧氏空间,两个复数对应4个实数变量。但是,因为这两个复数C1,C2的平方分别代表叠加态|y>被测量时,塌缩到本征态|0>和|1>的概率,因此C1,C2满足归一化条件,此外,可以忽略没有物理意义的整体相位,这样一来,便只剩下两个参数。被两个参数描述的所有叠加态,在4维空间中构成一个超曲面。更进一步,该超曲面对应于3维欧氏空间的一个球面,这就是布洛赫球面。
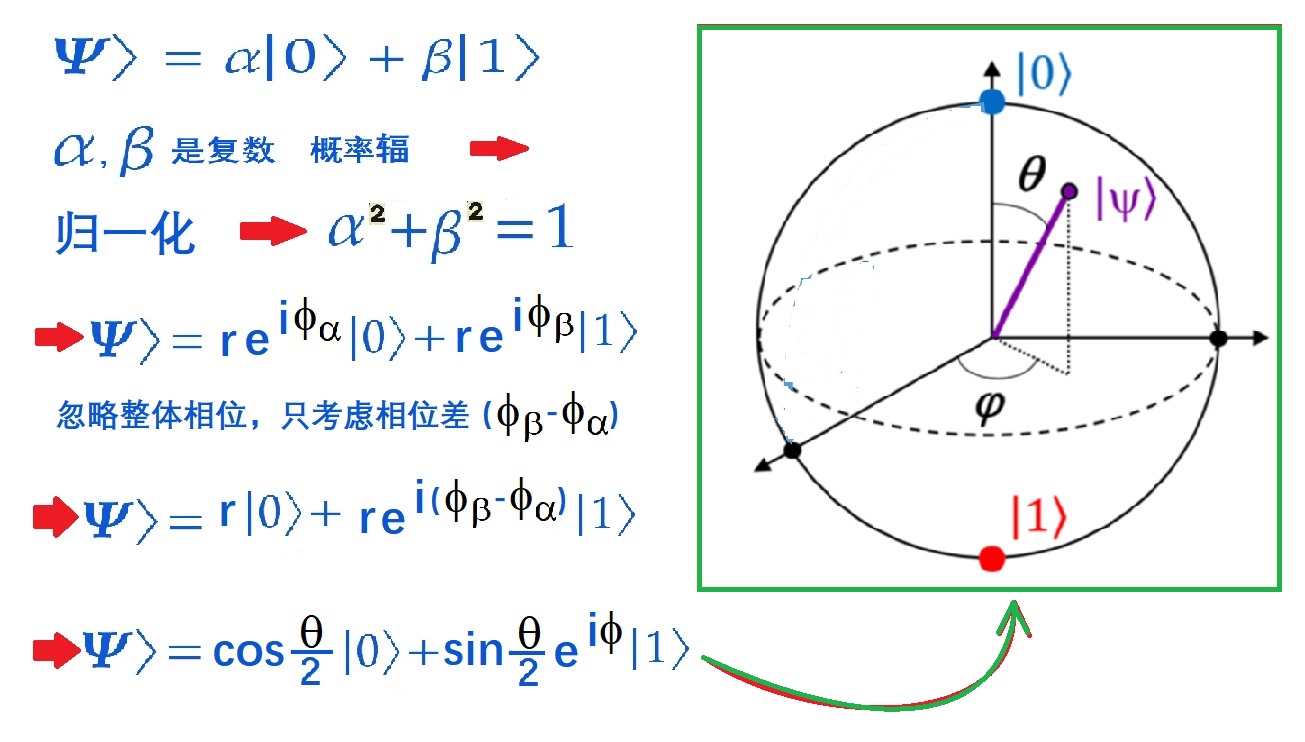
图3.2:布洛赫球面的来龙去脉
如图3.2所示,叠加态|y>可以表示为球面上的一个点:
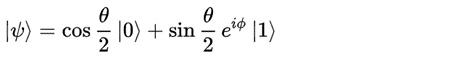
量子比特与比特,两者物理内容完全不同,具体实现也是天壤之别。比特用电压的高低两个值很容易实现,实现量子比特有多种方法,都非常困难。
比特只有两个状态是0和1,而量子比特的叠加态|y>有无穷多,因为布洛赫球面【4】上的任何点都是一个叠加态。每一个时刻,比特只有(0或1)1个值,而量子比特的叠加态同时有2个值。理解量子比特,是理解量子计算技术的关键。
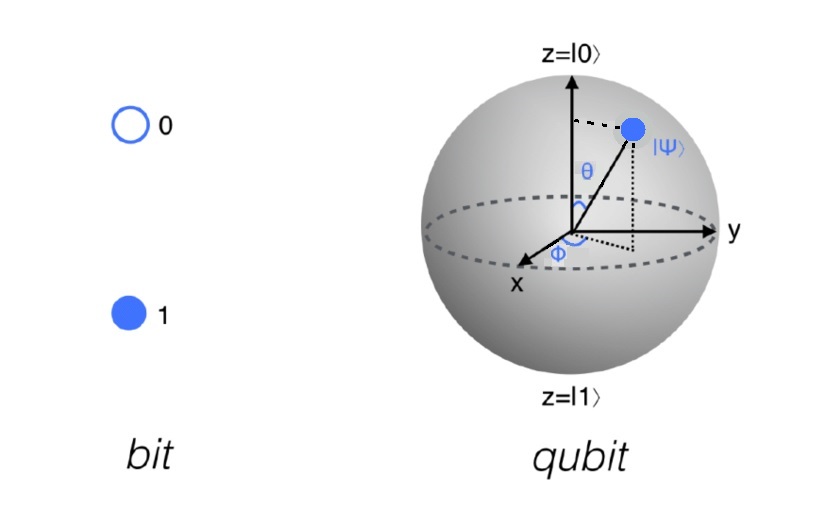
图3.3:比特和量子比特
叠加态作为量子比特,有两个关键点必须强调。
1,量子世界的本质是随机的,这个意思可以从本征态叠加态之关系理解。本征态和叠加态是相对的,依赖于物理量,也取决于(量子比特)基底的选择。例如对薛定谔的猫,一般我们说 “死猫”与“活猫”是基底,又死又活、半死不活是叠加态。然而这不是绝对的,也可以将又死又活 半死不活当作基底态,而“死猫” “活猫”便成为了叠加态,见图3.4。因此,原以为是固定态的基态,实质也是叠加态,所以本质上都是叠加态。
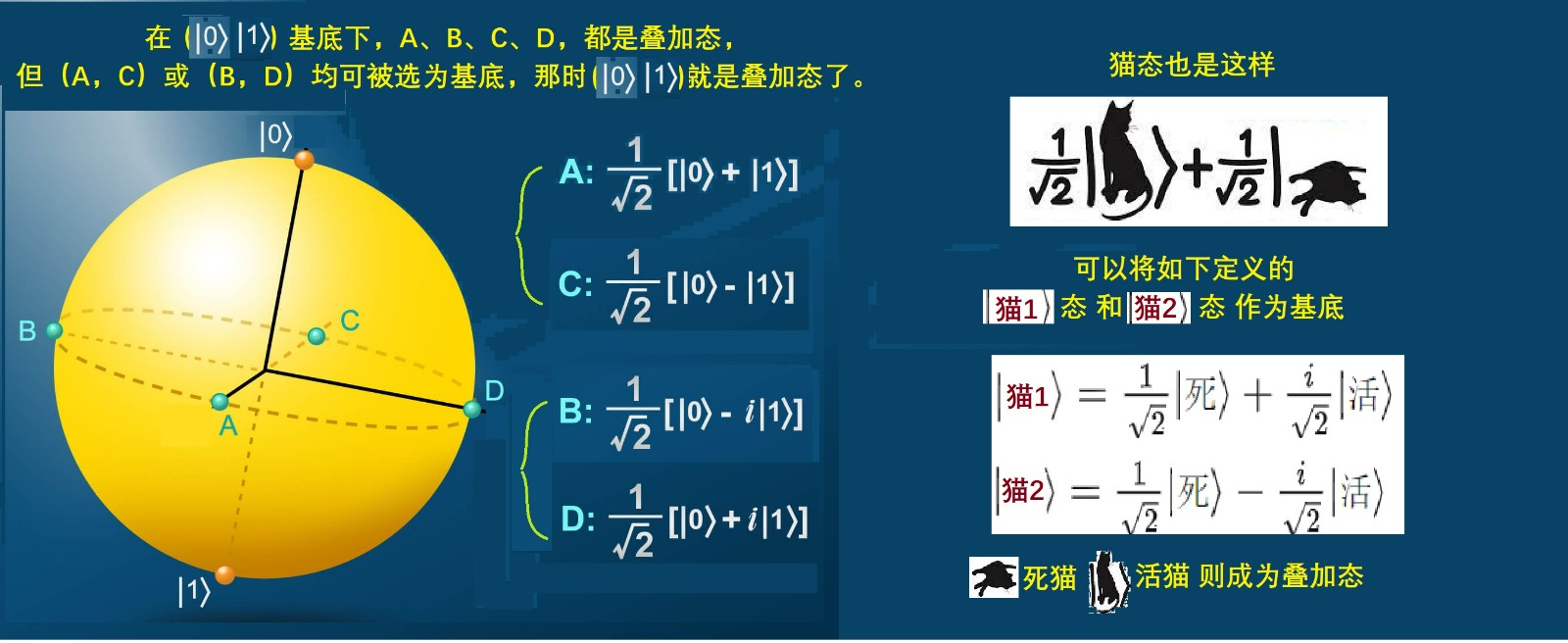
图3.4:叠加态和本征态是相对的
2,叠加态叠加什么?叠加的是概率幅不是概率。概率幅和概率是不一样的,它们的区别很重要。如果两个本征态互不正交,概率幅叠加会产生干涉项,见图3.5。概率幅叠加后,模的平方中,除了两个基态系数模之外,还有两个基态的相干项,包含了两个波函数相对相位的信息,即两个波函数是相干的。
而经典的概率叠加,仅是概率混合的统计现象。量子物理中概率幅的叠加,反映了波动的本质。量子叠加能产生干涉,多种状态同时存在,使得量子计算机能同时对多种状态进行计算,即可以对特定算法进行平行计算,这是量子计算快于经典计算的奥秘所在!
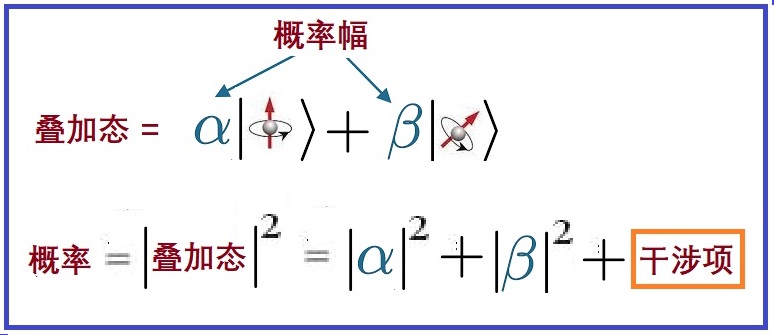
图3.5:概率幅叠加产生干涉项
机器的“计算”是什么意思呢?经典计算中有许多逻辑门:例如AND(与门),OR(或门),以及NOT(非门)与非门或非门等等。这些逻辑门的各种组合,将各个“比特”的0、1状态变来变去,便能够完成各种复杂的计算。量子比特也需要类似概念:“量子门”!量子门作用在Qubit的叠加态上,将Qubit变成另一个状态。
可以用2维矩阵代数的语言来描述叠加态(Qubit)的变化。量子比特是布洛赫球面上一个矢量,Qubit状态的演化,就是布洛赫球面上矢量的旋转。旋转是由用幺正(酉)矩阵表示的“量子门”引起的。矩阵(量子门)作用在矢量上,将Qubit的状态变成新的状态。许多Qubit、许多量子门连在一起,量子计算便如此一步一步进行下去。所有Qubit的最后状态,便是计算得到的最后结果。
(待续)
Contents
**** 1. 前言 ****
**** 2. 历史 ****
**** 3. 基础 ****
3.1 叠加态
3.2 量子比特
3.3 量子门
3.4 量子电路
**** 4. 算法 ****
4.1 Grover 量子搜索算法
4.2 多伊奇算法
4.3 秀尔算法-1(经典,数论部分)
4.4 秀尔算法-2(量子部分)
**** 5. 实现 ****
**********************************************************
作者部分YouTube视频:
https://www.youtube.com/watch?v=0I8FdazqAvc&list=PL6YHSDB0mjBKB2LBZDKL9UhcMMx6GtOsx
https://www.youtube.com/watch?v=_d0wquZkOYU&list=PL6YHSDB0mjBJ6qgfin-xKmP3FtTQr4x7i
*********************************************************
