《河图》的数字变化

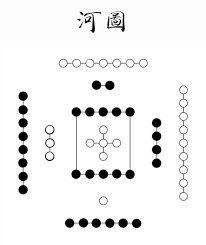
神秘的《河图》只不过是一个图形化的数学题，或者说是一个图形化的数字游戏，只是用图形描述了1到10十个数字的一种变化规律。它的精美之处在于其构图。那么这十个数字是如何变化的呢？

方法一：①将数字乘以9得到一个两位数，不足两位高位补0

     ②交换高低位数得到另一个两位数

     ③大的数和小的数之差除以9

计算如下：

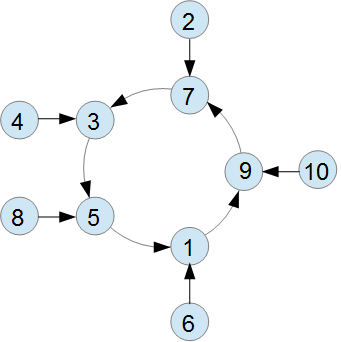
  1×9=09，90-09=81，81÷9=9。①→⑨

  9×9=81，81-18=63，63÷9=7。⑨→⑦

  7×9=63，63-36=27，27÷9=3。⑦→③

  3×9=27，72-27=45，45÷9=5。③→⑤

  5×9=45，54-45=09，09÷9=1。⑤→①。从此回到1，构成循环。

  2×9=18，81-18=63，63÷9=2。②→⑦。与9相同。

  4×9=36，63-36=27，27÷9=3。④→③。与7相同。

  6×9=54，54-45=09，09÷9=1。⑥→①。与5相同。

  8×9=72，72-27=45，45÷9=5。⑧→⑤。与3相同。

 10×9=90，90-09=81，81÷9=9。⑩→⑨。与1相同。

结果如图：

方法二：①将数字乘以9得到一个两位数，不足两位高位补0

     ②分解为两个一位数

     ③大的数减小的数

计算如下：

  1×9=09，9-0=9。①→⑨

  9×9=81，8-1=7。⑨→⑦

  7×9=63，6-3=3。⑦→③

  3×9=27，7-2=5。③→⑤

  5×9=45，5-4=1。⑤→①。从此回到1，构成循环。

  2×9=18，8-1=7。②→⑦。与9相同。

  4×9=36，6-3=3。④→③。与7相同。

  6×9=54，5-4=1。⑥→①。与5相同。

  8×9=72，7-2=5。⑧→⑤。与3相同。

 10×9=90，9-0=9。⑩→⑨。与1相同。

其实两个算法是一样的，因为如果一个任意两位数ab是9的倍数，则ba也是9的倍数，ab和ba的和、差同样是9的倍数，且以下等式成立：

    （ab+ba）÷9 = a+b

    （ab-ba）÷9 = a-b

奇偶组合一：

  将偶数与所变到的奇数组合则为：②⑦，④③，⑥①，⑧⑤，⑩⑨。

奇偶组合二：

  将变到相同数的奇数偶数组合则为：②⑨，④⑦，⑥⑤，⑧③，⑩①。在此组合中，奇偶数之和均为11。