费马大定理-铺平道路
怀尔斯证明了什么?人们都说怀尔斯证明了费马大定理,但是实际上,他证明的是 “模性定理”的一部分,就是我们在上篇中介绍的,原来叫“谷山-志村猜想”的那个。为什么证明了这个猜想就算证明了费马大定理呢?这是因为,有好几位数学家已经为通往费马大定理铺好了路……

1,儿时梦造就大师
今年的诺贝尔物理奖得主之一,是人工智能教父辛顿。据说他在少年时代就立志要弄懂“大脑是如何工作的?”,几经坎坷,他终于走到了正确的道路上并作出卓越的贡献。这样的事在科学史上屡见不鲜:爱因斯坦相对论的思想,也是源于他儿时的想象:如果自己骑在“光线”上旅行的话,对时间将有何种感受?
1922年,9岁的图灵读到一本《儿童应知道的自然奇观》,书中有句话“人体也是一台机器”,令儿时的图灵震撼,影响深远!他决定要探究人与机器之关系,最后愿望终于实现。四十年之后的1963年,我们的主角,10岁的安德鲁·怀尔斯(Andrew Wiles,1953-)初识费马大定理!一天,他偶去图书馆,翻看叫《大问题》的一本书,在书中邂逅了它!不料从此后怀尔斯便与其结下不解之缘。令怀尔斯颇感奇怪的是,这个定理很容易陈述,十岁的他就能理解,但却从来没有人证明过!这让他着迷,激发他的好奇心和好胜心,并且,他似乎当年就知道自己永远不会放弃它,必须解决它!
怀尔斯出生于英国剑桥,父亲原来是牧师,后来成为牛津大学神学教授。
怀尔斯后来就读于剑桥大学国王学院。1974 年,怀尔斯在牛津大学默顿学院获得数学学士学位。从 1975 年夏天,怀尔斯在约翰·科茨的指导下开始他的研究生阶段。他们一起用岩泽理论的方法研究椭圆曲线的复数乘法算法。他进一步与巴里·马祖尔合作研究了有理数上岩泽理论的主要猜想,不久之后,他将这个结果推广到全实数域。
1980 年,怀尔斯在剑桥大学克莱尔学院获得博士学位后,到新泽西州普林斯顿高等研究院任职,并于 1981 年成为普林斯顿大学数学教授。
怀尔斯的潜意识深处,总藏着费马猜想。但是,从70年代在剑桥大学开始,他就一直专门研究椭圆曲线,也取得不少成果,不过这看来与费马大定理没什么关系哦。
此时,两位日本数学家也已经提出了他们的猜想,并且,在美国的法国数学家韦伊(André Weil,1906-1998)的一篇论文将此猜想介绍到了西方,使得广为人知,韦伊还为猜想提供了概念性的证据,因此也被称为“谷山-志村-韦伊猜想”。该猜想企图将怀尔斯正在研究的椭圆曲线方程与模形式联系在一起。但没有人能证明这个猜想,即使被证明了,与费马大定理也没啥关系啊。
怀尔斯意识到自己的数论知识太有限了,也许要放弃这个儿时的梦想?历史的脚步很快就走到了80年代,怀尔斯33岁了。想不到这时候,数学界有几篇文章,引起了怀尔斯的注意,终于有人将费马的最后猜测,与他熟悉的椭圆曲线联系起来了!
2,弗雷曲线
格哈德·弗雷(Gerhard Frey,1944-)是德国数学家。他的研究领域是数论和丢番图几何,以其在数论方面的工作而闻名。他同时也研究椭圆曲线密码学,或许正因为如此,他第一个将费马猜想与椭圆曲线联系起来。
弗雷假设,如果费马方程有解,那么他就可以从费马方程的所谓解,构造出一个椭圆曲线。

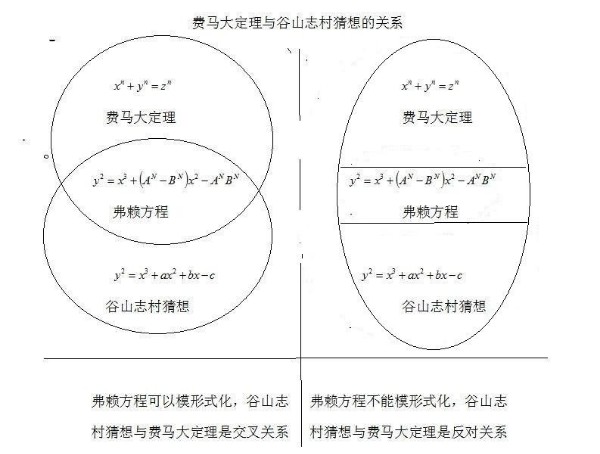
弗雷几年前就研究过类似的曲线,现在他注意到该曲线具有不寻常的性质,可能不是“模的”!这条曲线后来被称为弗雷曲线【1】。1985年,弗雷猜想这个费马大定理的反例将创造出一条非模的曲线,这样就在费马和谷山-志村猜想之间架起了一座桥梁。因此,弗雷提出谷山-志村猜想可能蕴含着费马大定理,这个想法引起了广泛的兴趣,也重新点燃怀尔斯儿时要“攻克费马最后猜想”的心灵之火。
怀尔斯当然暗地里兴奋不已,似乎费马大定理的证明有希望了:首先需要证明模定理,其次需要证明弗雷的直觉是正确的。
3,塞尔和黎贝
弗雷的研究虽然引起了一些关注,但距离费马大定理的证明还有十万八千里!因为上面说的都是猜想,这个猜想连着那个猜想,猜想都解决了,费马大定理才能解决。特别是那个谷山-志村的“模猜想“,当代的数学大师们都普遍认为这是无法证明的,太难了!至于弗雷的猜想,他只是给出了一种说法,说”这是可行的“,但没有给出完整的证明,弗雷并没有严格证明自己的猜想。
不过,不久之后,法国数学家让-皮埃尔·塞尔(Jean-Pierre Serre,1926年-)参与进来了【2】。他明确了弗雷所猜测的联系(图1中的蓝色箭头),又提出了一个ε猜想。并近乎完整的证明了:如果证明了谷山-志村猜想,又证明了ε猜想,那就意味着证明了费马大定理(图1中棕色虚线)。
让-皮埃尔·塞尔主要贡献的领域是拓扑学、代数几何与数论。他曾获颁许多数学奖项,包括1954年获得的菲尔兹奖。当时他年仅28岁,是至今最年轻的菲尔兹奖得主。他2000年获沃尔夫数学奖,2003年获阿贝尔奖,是阿贝尔奖的首个得主。他与格列戈里·马尔古利斯并列数学界“三大奖项”大满贯得主。
那好,现在所需证明的头绪清楚了:费马大定理=谷山-志村猜想+ε猜想。那么,塞尔的ε猜想说些什么呢?它的意思是说,如果与椭圆曲线相关的伽罗瓦表示具有某些特性,那么该曲线不能是模形式的。这儿的“伽罗瓦表示”,以及“某些特性”是什么特性,涉及太多的复杂数学概念,我们就无法深究了。总而言之,塞尔已经确保扫清了其它所有的障碍,只剩下“模”和“ε”两个猜想了。
这时,又一位叫黎贝的数学高手登场了,他解决了ε猜想【3】(黎贝定理),为最后证明费马大定理铺平了道路。
肯尼斯·黎贝(Kenneth Ribet,简称肯·黎贝,1948-),美国数学家,目前在柏克莱加州大学任教,研究领域涉及代数数论与代数几何。

图1:证明FLT
黎贝出生于纽约布鲁克林,父母均为犹太人。黎贝在法拉盛高中读书时,加入了竞争激烈的数学队,但他本科最开始学习的领域是化学。黎贝1973年从哈佛大学获得博士学位后,在普林斯顿大学任教三年,之后于1978 年,加入加州大学伯克利分校数学系。
黎贝于1986 年证明了ε猜想,所以现在它被叫做黎贝定理。此外还有至关重要的是,它还表明,为了证明费马大定理,不需要证明完整的谷山-志村猜想,只需证明一个特例,即半稳定椭圆曲线满足猜想,就足够了。弗雷曲线就是这种“半稳定椭圆曲线”。
而弗雷提出的联系也由黎贝证明了:如果用费马方程的解作为一组数,以这种方式构造椭圆曲线,则得到的椭圆曲线不能是模的。
所以,现在只剩下找出最后一个钥匙:只要能对“半稳定椭圆曲线”证明谷山-志村猜想,就自动证明了费马大定理。因为如果所有半稳定椭圆曲线都必须是模的,而黎贝定理又表明,费马方程的解创建的半稳定椭圆曲线是非模的。这两个陈述唯一可能为真,就是费马方程没有解,这样就无法创建这样的曲线。
不过,找到最后一个钥匙很难。30年来,所有企图证明谷山-志村猜想的努力,都以失败告终,即使是黎贝也说:“我甚至没有想到过要去试一下证明它”。大多数数学家都认为这是一块搬不动的大石头。
参考资料:
【1】Frey, Gerhard (1986), "Links between stable elliptic curves and certain Diophantine equations", Annales Universitatis Saraviensis. Series Mathematicae,
【2】Serre, Jean-Pierre (1987), "Sur les représentations modulaires de degré 2 de Gal(Q/Q)", Duke Mathematical Journal, 54 (1): 179–230
【3】Ribet, Ken (1990). "On modular representations of Gal(Q/Q) arising from modular forms" (PDF). Inventiones Mathematicae. 100 (2): 431–476.